. Jasio: W równoległoboku ABCD, w którym |AB| = 2|AD| punkt M jest srodkiem boku CD. Wykaz że trójkat ABM jest prostokatny. na początek może poproszę podpowiedź

rumpek: Taka podpowiedź powinna styknąć

Jasio: poddaje sie mozesz mi to wyłozyć

rumpek: To kolejna podpowiedź: Trójkąt MCB oraz trójkąt ADM są równoramienne, a co za tym idzie − 2 kąty są równe.

rumpek: Może teraz ? Jak coś mogę to udowodnić, żaden problem

Jasio: no juz wiem ale mozesz napisac rozwiązanie dla potomnych

rumpek: Oznaczmy sobie |∡BCM| = α. Skoro trójkąt MCB jest równoramienny zatem kąty |∡CMB| = |∡CBM| =

	180o − α
	2

Teraz rozpatrzmy trójkąt MDA, kąt |∡MDA| = 180^o − α (ponieważ w równoległoboku suma kątów ma

	α
miarę 180o). Czyli w trójkącie MDA kąt |∡ADM| = |∡MDA| =		.
	2

Suma kątów (kąt półpełny przy wierzchołku M) to 180^o, czyli:

	α		180o − α
180o = |∡AMB| +		+
	2		2

	α		α
180o = |∡AMB| +		+ 90o −
	2		2

|∡|AMB| = 90^o c.n.u.

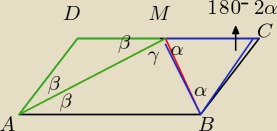
Aga1: Kąt MAB=kątowi AMB, bo kąty naprzemianległe są równe. 2β=180⁰−2α−−−−przeciwległe kąty w równoległoboku są równe. Stąd 2α+2β=180⁰ //:2 α+β=90⁰ α+β+γ=180⁰−−−−suma tych trzech kątów jest kątem półpełnym Podstawiając za α+β=90 mamy, że γ=90⁰